Standar deviasi adalah ukuran yang menjadi perhatian dalam banyak penelitian. Karena ukuran ini menunjukkan banyaknya data yang tersebar secara merata.
Pada pembahasan kali ini, Anda akan belajar rumus standar deviasi beserta penerapannya dalam soal.
Contents
Standar Deviasi dan Varian
Standar deviasi adalah ukuran untuk mengetahui data yang diteliti memiliki persebaran yang baik atau tidak.
Nilai standar deviasi juga disebut sebagai simpangan baku yang menunjukkan nilai ketidakpastian sebuah data yang dimiliki.
Nilai simpangan baku yang semakin kecil, maka nilai tersebut mendekati nilai rata-rata kelompok.
Namun jika nilai simpangan baku semakin besar, maka nilai-nilai dalam kelompok jauh dari nilai rata-rata kelompok.
Terdapat dua jenis nilai dalam standar deviasi atau simpangan baku:
- Nilai yang dekat dengan rata-rata
- Nilai yang jauh dengan rata-rata
Nilai yang mendekati nilai rata-rata kelompok menunjukkan bahwa semua data memiliki keseragaman nilai yang tidak berbeda jauh.
Sedangkan jika nilai menjauhi nilai rata-rata kelompok, maka terdapat nilai dalam kelompok tidak tersebar merata serta tumpang.
Sehingga nilai dalam kelompok yang aneh atau biasa dikenal dengan outlier, dapat dibuang atau tidak dimasukkan dalam perhitungan sehingga nilai anggota kelompok mendekati nilai rata-rata kelompok yang diteliti.
Baca Juga: Rumus Panjang Gelombang
Pada umumnya standar deviasi atau simpangan baku disimbolkan dalam bentuk s atau σ.
Rumus Standar Deviasi
Nilai suatu standar deviasi atau simpangan baku bergantung terhadap nilai varian yang didapatkan.
Dikarenakan hubungan antara simpangan baku dan varian adalah akar dari varian. Sehingga rumus yang digunakan seperti di bawah ini.
1. Rumus Standar Deviasi Data Kelompok untuk Populasi
Rumus pertama ini digunakan jika varian berbentuk seperti di bawah ini.
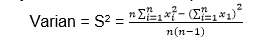
Sehingga rumus standar deviasinya adalah sebagai berikut.
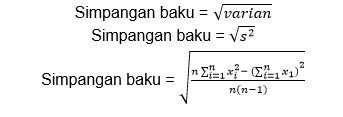
2. Rumus Standar Deviasi Data Tunggal
Rumus kedua digunakan jika menemukan bentuk varian seperti di bawah ini.
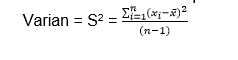
Sehingga rumus standar deviasinya adalah sebagai berikut ini.

Contoh Soal dan Penyelesaian Standar Deviasi
Soal 1
Diketahui dalam 4 tahun berturut-turut semenjak 2007 hingga 2010, pertumbuhan laju ekonomi Indonesia adalah 4,5%, 5%, 5,5%, dan 5%. Tentukan nilai standar deviasi dari pertumbuhan laju ekonomi Indonesia
Untuk mengerjakan soal di atas, cara pertama yang bisa dilakukan adalah mencari nilai rata-rata dari laju pertumbuhan ekonomi Indonesia seperti di bawah ini.
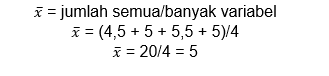
Rumus standar deviasi yang bisa digunakan adalah rumus standar deviasi data tunggal sehingga bisa dikerjakan seperti di bawah ini.

Soal 2
5 orang siswa telah diukur berat badannya yaitu 45 kg, 43 kg, 42 kg, 41 kg, dan 65 kg. Tentukan nilai standar deviasi dari berat badan 5 orang siswa.
Cara mengerjakan sama seperti nomor 1, cari rata-rata terlebih dahulu kemudian cari nilai standar deviasi.

Standar deviasi ini tidak hanya digunakan dalam ilmu statistika saja, namun juga bisa digunakan dalam bidang fisika.
Dari penjelasan di atas juga, disimpulkan bahwa standar deviasi erat kaitannya dengan simpangan baku.

2 thoughts on “Rumus Standar Deviasi”